graph_tool.centrality.closeness#
- graph_tool.centrality.closeness(g, weight=None, source=None, vprop=None, norm=True, harmonic=False)[source]#
Calculate the closeness centrality for each vertex.
- Parameters:
- g
Graph Graph to be used.
- weight
EdgePropertyMap, optional (default: None) Edge property map corresponding to the weight value of each edge.
- source
Vertex, optional (default:None) If specified, the centrality is computed for this vertex alone.
- vprop
VertexPropertyMap, optional (default:None) Vertex property map to store the vertex centrality values.
- normbool, optional (default:
True) Whether or not the centrality values should be normalized.
- harmonicbool, optional (default:
False) If true, the sum of the inverse of the distances will be computed, instead of the inverse of the sum.
- g
- Returns:
- vertex_closeness
VertexPropertyMap A vertex property map with the vertex closeness values.
- vertex_closeness
See also
central_point_dominancecentral point dominance of the graph
pagerankPageRank centrality
eigentrusteigentrust centrality
eigenvectoreigenvector centrality
hitsauthority and hub centralities
trust_transitivitypervasive trust transitivity
Notes
The closeness centrality of a vertex \(i\) is defined as,
\[c_i = \frac{1}{\sum_j d_{ij}}\]where \(d_{ij}\) is the (possibly directed and/or weighted) distance from \(i\) to \(j\). In case there is no path between the two vertices, here the distance is taken to be zero.
If
harmonic == True, the definition becomes\[c_i = \sum_j\frac{1}{d_{ij}},\]but now, in case there is no path between the two vertices, we take \(d_{ij} \to\infty\) such that \(1/d_{ij}=0\).
If
norm == True, the values of \(c_i\) are normalized by \(n_i-1\) where \(n_i\) is the size of the (out-) component of \(i\). Ifharmonic == True, they are instead simply normalized by \(V-1\).The algorithm complexity of \(O(V(V + E))\) for unweighted graphs and \(O(V(V+E) \log V)\) for weighted graphs. If the option
sourceis specified, this drops to \(O(V + E)\) and \(O((V+E)\log V)\) respectively.If enabled during compilation, this algorithm runs in parallel.
References
[closeness-wikipedia][opsahl-node-2010]Opsahl, T., Agneessens, F., Skvoretz, J., “Node centrality in weighted networks: Generalizing degree and shortest paths”. Social Networks 32, 245-251, 2010 DOI: 10.1016/j.socnet.2010.03.006 [sci-hub, @tor]
[adamic-polblogs]L. A. Adamic and N. Glance, “The political blogosphere and the 2004 US Election”, in Proceedings of the WWW-2005 Workshop on the Weblogging Ecosystem (2005). DOI: 10.1145/1134271.1134277 [sci-hub, @tor]
Examples
>>> g = gt.collection.data["polblogs"] >>> g = gt.GraphView(g, vfilt=gt.label_largest_component(g)) >>> c = gt.closeness(g) >>> gt.graph_draw(g, pos=g.vp["pos"], vertex_fill_color=c, ... vertex_size=gt.prop_to_size(c, mi=5, ma=15), ... vcmap=matplotlib.cm.gist_heat, ... vorder=c, output="polblogs_closeness.pdf") <...>
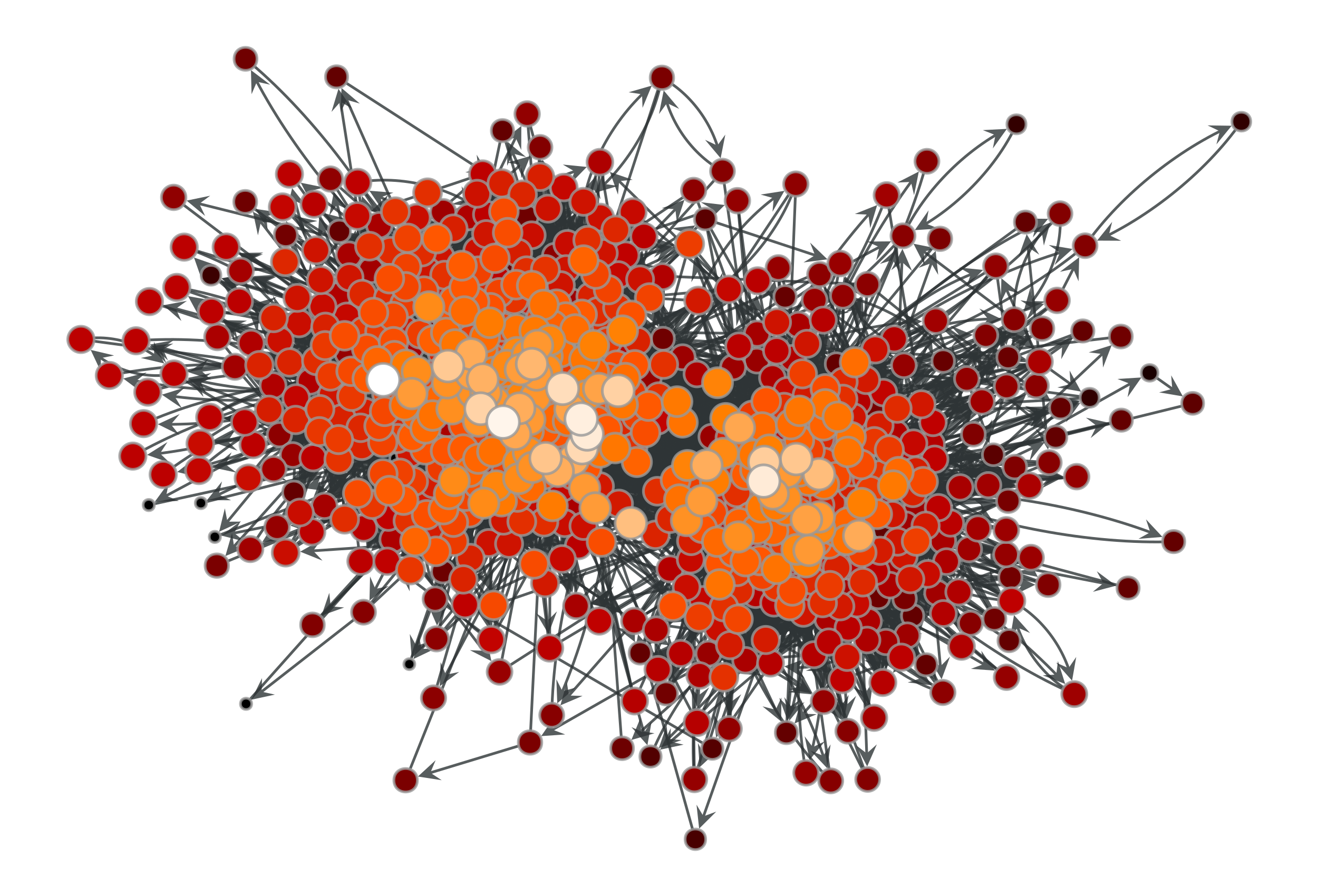
Closeness values of the a political blogs network of [adamic-polblogs].#